Aspettando il picco dei contagi, che potrebbe essere già arrivato
Quando arriverà il picco dovuto al lockdown di tutta Italia? Quando inizieranno a scendere i numeri? Quando inizieremo a vedere il "dopo"?
Il dubbio è che il "dopo" sia già arrivato.
Epidemia e contenimento
Semplificando all'estremo ci sono due regimi per la diffusione di una malattia contagiosa nella sua fase iniziale:
- l'epidemia, quando il contagio cresce esponenzialmente e le persone infette raddoppiano con un tempo caratteristico,
- il contenimento, quando il contagio decresce esponenzialmente e le persone infette dimezzano con un tempo caratteristico.
La differenza tra i due regimi è data dal numero di persone infettate da ciascuna infetta che nei modelli matematici è chiamato "effective reproduction number" o R, quando questo numero è maggiore di uno (R > 1) siamo nel regime epidemico in cui il contagio segue la legge della reazione a catena simile a quella che si genera in una esplosione nucleare. Quando R è minore di uno (R < 1) siamo nella fase di contenimento.
Questo è quello che si è visto nella provincia cinese di Hubei, il contagio è cresciuto esponenzialmente fino al momento in cui il 23 gennaio le autorità hanno imposto il ferreo lockdown, ossia la chiusura di tutte le attività e l'obbligo per tutte le persone di non uscire di casa se non per fare la spesa. Questo ha ridotto al minimo i contatti tra le persone e di conseguenza la possibilità per gli infetti di contagiare persone al di fuori della propria abitazione. Oltre al lockdown sono state prese altre misure in particolare la ricerca e l'isolamento di tutti i contatti di tutte le persone trovate "positive" al virus. In breve tempo il numero di nuovi casi giornalieri è crollato e con i tempi tipici della malattia gli ospedali si sono svuotati.
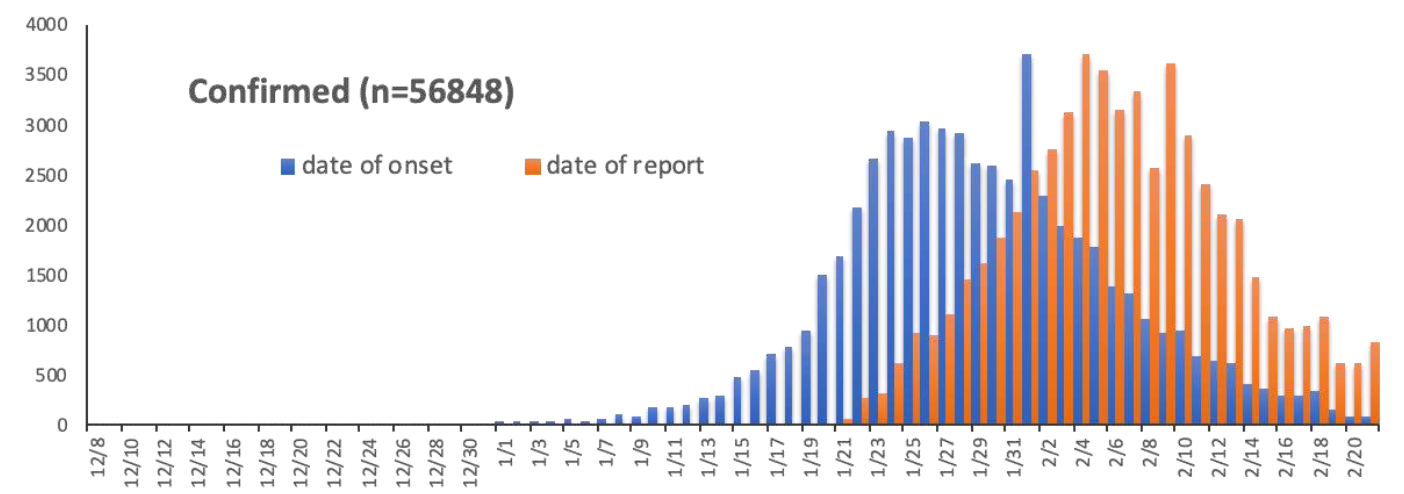
Questo è il razionale delle misure di "distanziamento sociale" e di lockdown prese in Italia e nel resto del mondo, portare R sotto a uno come in Cina e vedere la curva del contagio scendere.
L'attesa del contenimento in Italia
Ma l'attesa del picco in Italia e non solo si sta facendo lunga. Ben più lunga che che a Hubei.
Perché?
Tutti i parametri sanitari a livello nazionale, il numero di persone ricoverate in ospedale, il numero di pazienti in terapia intensiva e il numero giornaliero di decessi si sono stabilizzati nella seconda metà di Marzo, ma non accennano a diminuire.
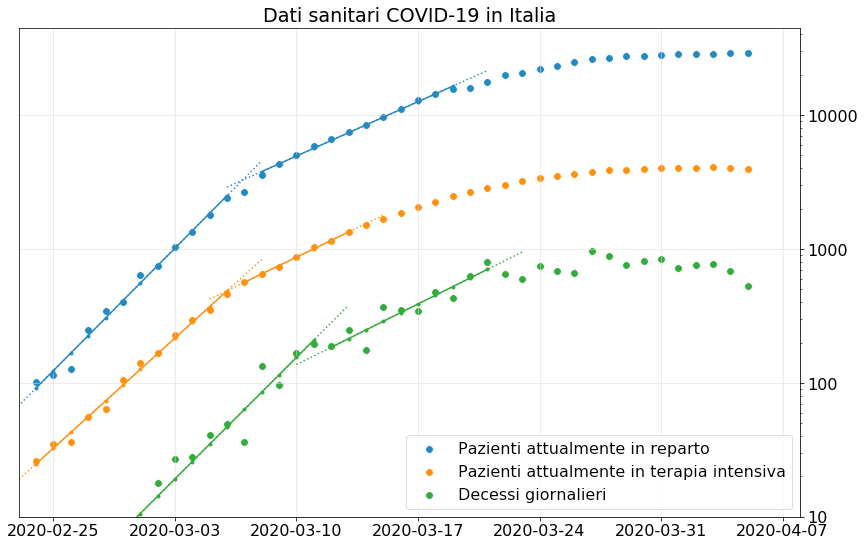
In molti seguiamo giornalmente le conferenze stampa della Protezione Civile attendendo il momento in cui inizieranno a diminuire il numero di morti. Finora senza soddisfazione.
Sappiamo che i dati nazionali non sono particolarmente affidabili a causa delle anomalie registrate in Lombardia, ma i dati di numerose regioni che non risultano in crisi presentano esattamente la stessa caratteristica: stabilizzazione dei numeri, ma non una discesa dopo un chiaro massimo.
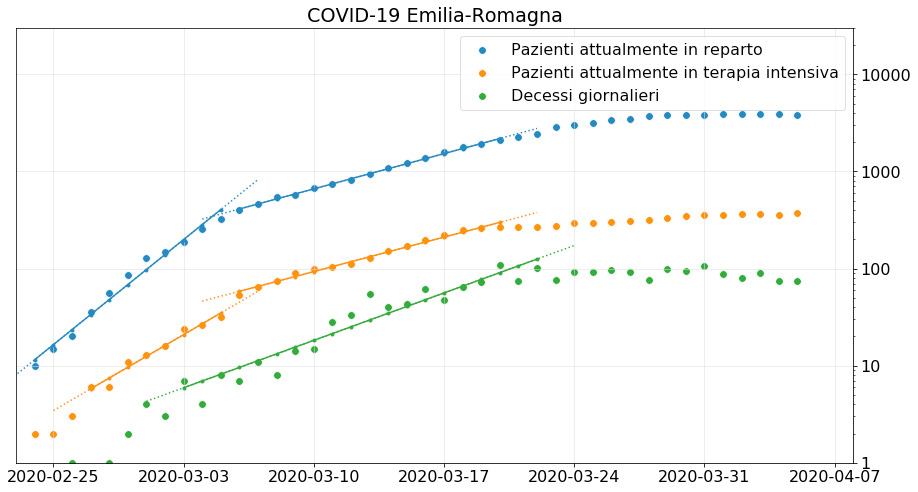
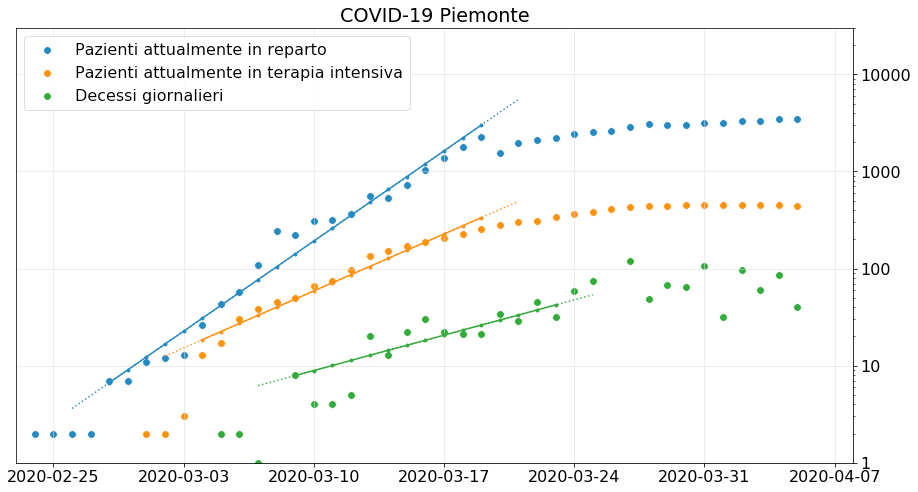
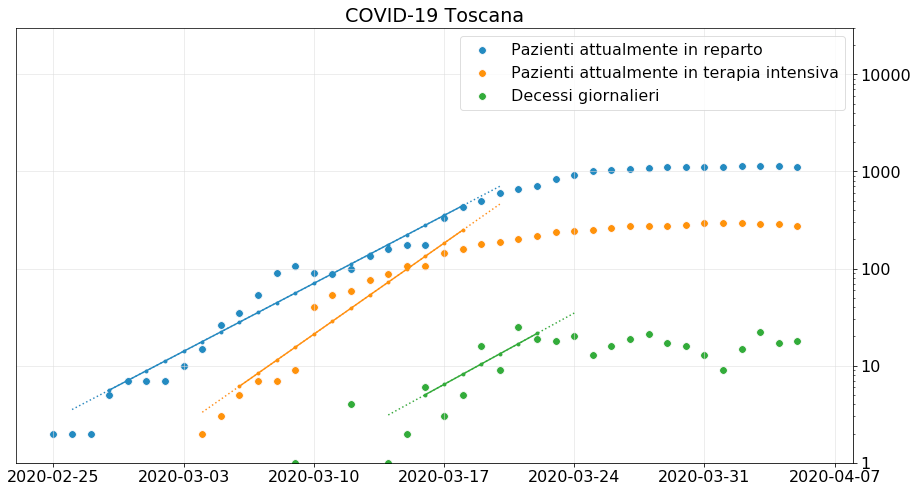
Come è possibile che non siamo più in crescita esponenziale ma nemmeno in diminuzione?
Ancora peggio, come è possibile che tutti i dati siano rimasti così stabili?
Negli ultimi tempi mi sentivo di non capire. Per questo sono stato meno attivo su Facebook. Non avevo niente di interessante da dire.
La cosa ancora più sconcertante è che questa stabilizzazione si osserva anche nei dati di molti altri Paesi. Alla crescita esponenziale non segue una decrescita, ma una crescita lineare: Corea del Sud, Giappone, Spagna e altri.
Lo scenario a R = 1
Invece ora ho trovato uno scenario che spiegherebbe questa apparente sospensione e purtroppo non è per niente piacevole.
La situazione attuale sembra descritta dal caso in cui il numero di infetti cambia lentamente, ossia R = 1, che nei modelli matematici non viene considerato in quanto "instabile".
Ma la realtà non è un modello matematico e R in realtà varia di comune in comune, di quartiere in quartiere e anche tra una persona e l'altra, perché dipende dai comportamenti individuali e sociali.
E i comportamenti delle persone variano se nella propria area sia in corso un focolaio o meno, se corre voce che ci siano colleghi, vicini o parenti "positivi" o meno.
Lo scenario che mi sembra possa spiegare meglio questo stato "pseudo-stabile" è che le misure restrittive al momento garantiscano che in generale R sia vicino a 1 ma leggermente superiore. In questa maniera possono partire focolai a crescita esponenziale, anche se lenta, in alcune aree fino al momento in cui le prime persone iniziano a stare male. A quel punto si diffonde la notizia che nell'area ci sono dei contagi e tutti si allertano, cambiano le abitudini, diminuiscono le interazioni abbastanza da rendere R negativo e spegnere il focolaio.
Ma nel frattempo alcune delle persone contagiate avranno acceso almeno un altro focolaio in un'altra area, dove la tensione è più bassa e via di seguito.
L'idea quindi è che possa esistere un meccanismo di autocontrollo dei comportamenti sociali che mantiene R = 1 in media nelle diverse regioni. I contagi non rimarrebbero davvero stabili ma oscillerebbero nel tempo senza una tendenza a crescere o a diminuire.
Questo scenario ha delle implicazioni molto pesanti.
Questo sarebbe già il "dopo".
Se questa fosse la spiegazione, significa che le regole del lockdown all'italiana attuale non sono sufficienti a garantire R < 1 come a Hubei. Se non vengono prese ulteriori misure di contenimento, penso in particolare al tracciamento dei contatti dei "positivi" e alla quarantena individuale, il rischio è di rimanere tutti a casa fino a data da destinarsi.
Col solito conto spannometrico 600 morti al giorno all'1% di mortalità significherebbe che ci sono circa 60.000 nuovi infetti al giorno, lo 0.1% della popolazione. Questo numero sembra gestibile dal sistema sanitario nazionale.
Ma dovremmo stare a casa più di due anni per raggiungere un'immunità diffusa.
Chi fosse interessato ai prossimi aggiornamenti può seguirmi su Facebook.
Se vuoi mettere un like, condividere o discutere questo articolo su Facebook l'annuncio è qui.
Area per i data nerd
Il modello più semplice per descrivere matematicamente l'epidemia di COVID-19 è il modello Susceptible-Infectious-Recovered o SIR i cui dettagli sono ben descritti in questo video di Numberphile e le approssimazioni di cui sopra sono buone finché il numero la percentuale di suscettibili è vicina al 100%.
Matematicamente parlando la tesi di questo articolo è che le disomogeneità di R e il feedback negativo locale possano rendere il regime "instabile" a R = 1 "pseudo-stabile".
Tutto il mio codice e i notebook sono disponibili su Github.
